- Strypo varžą galima rasti pagal formulę: \(R=\rho\frac{l}{S}\) , kur \(\rho\) — savitoji geležies varža, \(l\) — strypo ilgis, \(S\) jo skerspjūvio plotas. Strypo ilgį galima sužinoti iš formulės: \(l=\frac{4m}{\pi d^{2}\rho_{\text{gel}}}\) , kur \(\rho_{\text{gel}}\) yra geležies tankis.Skerspjūvio plotas apskaičiuojamas pagal \(S=\pi\frac{d^{2}}{4}\) Taigi geležinio strypo varžą galima apskaičiuoti pagal: \(R=\rho\frac{16m}{\pi^{2}d^{4}\rho_{\text{gel}}}=1{,}8\;\text{m}\Omega\)
- \[ R=\rho\frac{l}{S} \] \(m=\rho_{\text{var}}lS\) , čia \(\rho_{\text{var}}\) — vario tankis, \(\rho\) — vario savitoji varža.Iš šių formulių galima išsireikšti ieškomus dydžius: \(l=\sqrt{\frac{mR}{\rho_{\text{var}}\rho}}=340\;\text{m}\) \(S=\sqrt{\frac{\rho m}{\rho_{\text{var}}R}}=1{,}0\cdot10^{-7}\;\text{m}^2\)
- Visų pirma išnagrinėkime schemą, parodytą paveikslėlyje a. matome, kad šioje schemoje ampermetras yra prijungtas nuosekliai su rezistoriumi. Taip sujungtas ampermetras rodo teisingus parodymus, jis išmatuoja elektros srovės stiprį \(I_{\text{A}} = I_{x}\), tekančią per rezistorių. Tačiau, voltmetras nėra prijungtas paraleliai rezistoriui ir todėl jo parodymai „meluoja“: jis matuoja ne rezistoriaus įtampą, o bendrą rezistoriaus (\(U_x\)) ir ampermetro (\(U_{\text{A}}\)) įtampą. Iš to seka, kad: \(\frac{U}{I}=\frac{U_{\text{A}}+U_{x}}{I}=\frac{U_{\text{A}}}{I_{\text{A}}}+\frac{U_{x}}{I_{x}}=R_{\text{A}}+R_{x}\) ,Taigi \(\frac{U}{I}\) santykis yra lygus rezistoriaus ir ampermetro varžų sumai. Tokiu atveju, matuojant pagal šią schemą bus daromos mažos paklaidos, jeigu \(R_{\text{A}}\ll R_{x}\) (šiuo atveju, voltmetro varža neegzistuoja). Analogiškai išnagrinėjus b schemą, gauname, kad \(\frac{U}{I}=R_{x}\frac{R_{\text{V}}}{R_{x}+R_{\text{V}}}\) Šiuo antruoju atveju, matavimai bus ganėtinai tikslūs, jei \(R_{\text{V}}\gg R_{x}\) (ampermetro varža neegzistuoja).Išaanalizavus abejus atvejus, matome, kad mažoms \(R_x\) varžoms yra tinkama b schema, o didelėms \(R_x\) — a schema.
- Galima pradėti nuo voltmetro varžos išmatavimo (žr. pav. a): \[ R_{\text{V}}=\frac{U_{1}}{I_{2}} \] Tada, Rx varžos radimui galima naudotis pav. b pavaizduota schema: \[ R_{x}=\frac{U_{2}}{I_{2}-\frac{U_{2}}{R_{\text{V}}}}=\frac{U_{2}U_{1}}{U_{1}I_{2}-U_{2}I_{1}} \]
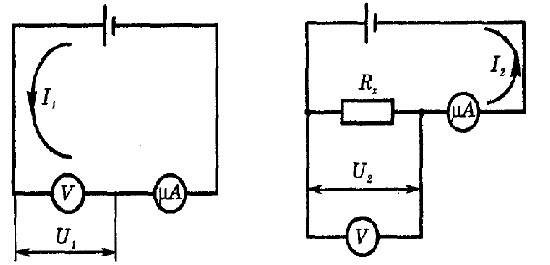Tokiu metodu galima naudotis tik tokiu atveju, kai yra naudojamas pakankamai jautrus ampermetras, galintis išmatuoti mažas sroves \(I_1\) ir \(I_2\). - Iš viso galima gauti 15 skirtingų R reikšmių: \(R=\frac{R_{0}}{4}=1{,}5\;\Omega\) ; \(R=\frac{R_{0}}{3}=2\;\Omega\) ; \(R=\frac{2R_{0}}{5}=2{,}4\;\Omega\) ; \(R=\frac{R_{0}}{2}=3\;\Omega\) ; \(R=\frac{3R_{0}}{5}=3{,}6\;\Omega\) ; \(R=\frac{2R_{0}}{3}=4\;\Omega\) ; \(R=\frac{3R_{0}}{4}=4{,}5\;\Omega\) ; \(R=R_{0}=6\;\Omega\) ; \(R=\frac{4R_{0}}{3}=8\;\Omega\) ; \(R=\frac{3R_{0}}{2}=9\;\Omega\) ; \(R=\frac{5R_{0}}{3}=10\;\Omega\) ; \(R=2R_{0}=12\;\Omega\) ; \(R=\frac{5R_{0}}{2}=15\;\Omega\) ; \(R=3R_{0}=18\;\Omega\) ; \(R=4R_{0}=24\;\Omega\)
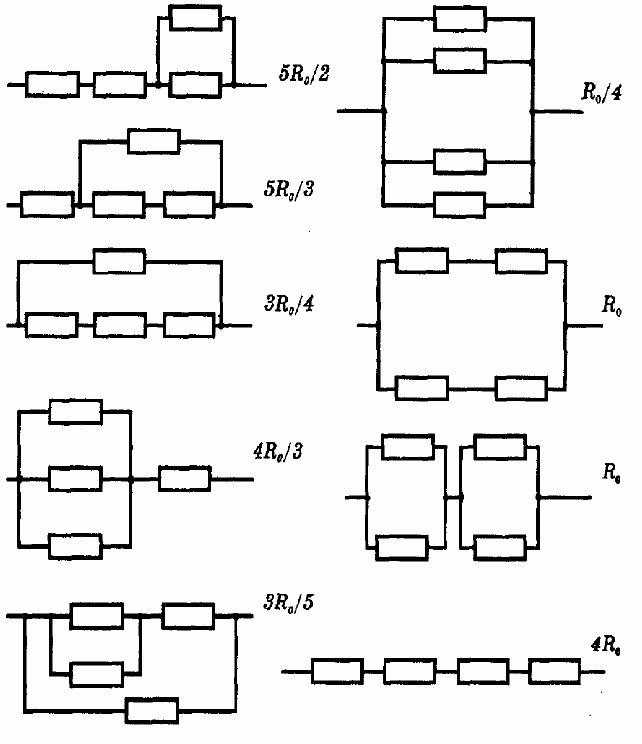Varžas \(R_0\), \(2R_0\), \(\frac{R_{0}}{2}\) , \(3R_0\), \(\frac{R_{0}}{3}\) , \(\frac{2R_{0}}{3}\) , \(\frac{3R_{0}}{2}\) galima gauti naudojant vieną, du ar tris rezistorius, šių schemų mes nepateikėme. Visos kitos schemos brėžinyje. - Visų pirma, būtina nustatyti, kaip yra sujungti rezistoriai grandinėje. Rezistoriai \(R_2\), \(R_4\), \(R_5\) yra sujungti grandinėje nuosekliai, todėl jų varža yra \(R_{245}=R_{2}+R_{4}+R_{5}=30\;\Omega\) . Rezistorius \(R_3\) yra sujungtas lygiagrečiai su \(R_{245}\), todėl \(R_{2345}=\frac{R_{3}R_{245}}{R_{3}+R_{245}}=12\;\Omega\) . Rezistoriai \(R_1\) ir \(R_6\) yra sujungti nuosekliai su \(R_{2345}\) ir, tokiu atveju, pilnutinė grandinės varža yra \(R=R_{1}+R_{6}+R_{2345}=18\;\Omega\) Pilnutinis grandinės elektros srovės stipriui apskaičiuoti naudojamės Omo dėsnio išraiška, tai \(I=\frac{U}{R}=2\;\text{A}\) Kadangi \(R_1\) ir \(R_6\) rezistoriai yra nešakotoje grandinės dalyje, pro juos teka visa elektros srovė, t.y. \(I_{1}=I_{6}=2\;\text{A}\). \(R_3\) — \(R_{245}\) dalyje elektros srovė išsiskirsto (srovės stipris kiekvienoje lygiagrečioje grandinės šakoje yra atvirkščiai proporcingas tos šakos varžai). Norint surasti elektros srovės stiprį kiekvienoje iš grandinės šakų, galima sudaryti atitinkamą proporciją. Galimas ir kitas sprendimo būdas — rasti vienos iš lygiagrečios grandinės šakos įtampą \(U_{3}=I\cdot R_{2345}=24\;\text{V}\). Tada, pagal Omo dėsnį \(I_{3}=\frac{U_{3}}{R_{3}}=1{,}2\;\text{A}\); \(I_{2}=I_{4}=I_{5}=\frac{U_{3}}{R_{245}}=0{,}8\;\text{A}\). Kaip ir turėtų būti \(I=I_{2}+I_{3}\)
- Galimų schemų su dvejais rezistoriais nėra daug ir paprastu būdu galima patikrinti, kad nei viena iš jų neatitinka uždavinio sąlygų. Galimų schemų su trimis rezistoriais taip pat nėra daug. Uždavinio sąlygas gali patenkinti tik du rezistorių sujungimo atvejai, parodyti a ir b paveikslėlyje. Parodysime, kad šios dvi jungimo schemos tenkina uždavinio sąlygą ir rasime atitinkamas rezistorių varžas .
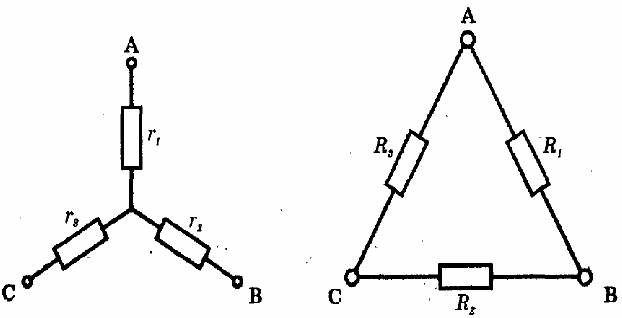
pav. a pav. b Pirmuoju atveju (pav. a), sujungus bet kuriuos du gnybtus, du atitinkami rezistoriai bus sujungti nuosekliai, todėl \(R_{\text{AB}}=r_{1}+r_{2}\) , \(R_{\text{BC}}=r_{2}+r_{3}\) , \(R_{\text{AC}}=r_{1}+r_{3}\) . Iš čia: \(r_{1}=\frac{R_{\text{AB}}+R_{\text{AC}}-R_{\text{BC}}}{2}=3\;\Omega\) \(r_{2}=\frac{R_{\text{AB}}+R_{\text{BC}}-R_{\text{AC}}}{2}=2\;\Omega\) \(r_{3}=\frac{R_{\text{BC}}+R_{\text{AC}}-R_{\text{AB}}}{2}=6\;\Omega\) Antruoju atveju (pav. b), sujungus bet kuriuos du gnybtus, vienas rezistorius bus sujungtas lygiagrečiai su kitais dviem atitinkamais rezistoriais, kurie tarpusavyje yra sujungti nuosekliai. Tokiu atveju: \[ R_{\text{AB}}=\frac{R_{1}(R_{2}+R_{3})}{R_{1}+R_{2}+R_{3}} \] \[ R_{\text{BC}}=\frac{R_{2}(R_{1}+R_{3})}{R_{1}+R_{2}+R_{3}} \] \[ R_{\text{AC}}=\frac{R_{3}(R_{2}+R_{1})}{R_{1}+R_{2}+R_{3}} \] Padalijus kiekvieną iš šių lygčių iš \(R_1 + R_2 + R_3\) ir sudėjus visas tris lygtis gausime: \[ R_{1}R_{2}+R_{1}R_{3}+R_{2}R_{3}=\frac{R_{\text{AB}}+R_{\text{BC}}+R_{\text{AC}}}{2}\left(R_{1}+R_{2}+R_{3}\right) \] Tada \[ R_{1}R_{2}=\frac{R_{\text{AB}}+R_{\text{BC}}-R_{\text{AC}}}{2}\left(R_{1}+R_{2}+R_{3}\right) \] \[ R_{2}R_{3}=\frac{R_{\text{BC}}+R_{\text{AC}}-R_{\text{AB}}}{2}\left(R_{1}+R_{2}+R_{3}\right) \] \[ R_{1}R_{3}=\frac{R_{\text{AB}}+R_{\text{AC}}-R_{\text{BC}}}{2}\left(R_{1}+R_{2}+R_{3}\right) \] Padalijus šias lygtis vieną iš kitos, rasime nežinomų varžų santykius: \[ \frac{R_{2}}{R_{1}}=\frac{R_{\text{BC}}+R_{\text{AC}}-R_{\text{AB}}}{R_{\text{AB}}+R_{\text{AC}}-R_{\text{BC}}}=2 \] \[ \frac{R_{3}}{R_{1}}=\frac{R_{\text{BC}}+R_{\text{AC}}-R_{\text{AB}}}{R_{\text{AB}}+R_{\text{BC}}-R_{\text{AC}}}=3 \] Įstačius \(R_{2}=2R_{1}\) ir \(R_{3}=3R_{1}\) į vieną iš sistemos lygčių, randame ieškomus dydžius: \(R_{1}=6\;\Omega\) , \(R_{2}=12\;\Omega\) , \(R_{3}=18\;\Omega\)
- Pasirenkame srovių kryptis atskirai grandinės daliai, kaip parodyta brėžinyje:
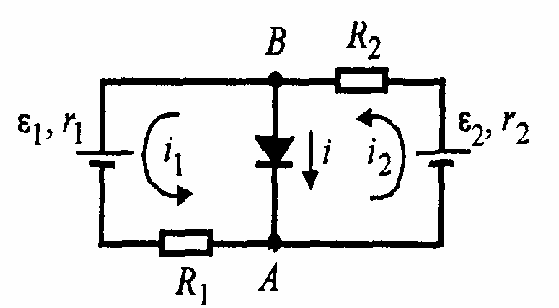Naudosime pirmąją Kirchofo taisyklę mazgui A, o antrąją Kirchofo taisyklę — BA\(\varepsilon_1\) ir B\(\varepsilon\)2A: \begin{align*} i_{2}-i_{1}&=i \\ i_{1}(r_{1}+R_{1})-ir_{0}&=-\varepsilon_{1}\\ i_{2}(r_{2}+R_{2})+ir_{0}&=-\varepsilon_{2}\end{align*} Čia \(r_0\) — diodo varža pirmosios krypties atveju.Išsprendus gautąją lygčių sistemą, randame \[ i=\frac{\varepsilon_{1}\left(r_{2}+R_{2}\right)-\varepsilon_{2}\left(r_{1}+R_{1}\right)}{r_{0}\left(r_{1}+R_{1}+r_{2}+R_{2}\right)+\left(r_{1}+R_{1}\right)\left(r_{2}+R_{2}\right)}<0\] Atlikę šiuos pakeitimus, gausime, kad srovė yra: \[i=\frac{\varepsilon_{2}\left(r_{1}+R_{1}\right)-\varepsilon_{1}\left(r_{2}+R_{2}\right)}{r_{0}\left(r_{1}+R_{1}+r_{2}+R_{2}\right)+\left(r_{1}+R_{1}\right)\left(r_{2}+R_{2}\right)}\approx5\cdot10^{-4}\;\text{A}\] - Srovė, pagal Omo dėsnį visai grandinei, yra randama pagal formulę: \(I=\frac{\varepsilon}{r+R}\) , kur \(\varepsilon\) — elektrovara, \(r\) — vidinė šaltinio varža, \(R\) — apkrovos varža.Šiuo atveju, išsiskiria galia: \(P=I^{2}R\) , iš kur galima išsireikšti, jog \(R=P/I^{2}\) .Įrašius R į srovės formulę ir šią formulę užrašius abiems atvejams, galima sudaryti lygčių sistemą: \begin{align*} I_{1}&=\frac{\varepsilon}{r+P_{1}/I_{1}^{2}}\\ I_{2}&=\frac{\varepsilon}{r+P_{2}/I_{2}^{2}}\end{align*} Išsprendus lygčių sistemą, randame ieškomą elektrovaros jėgos vertę: \(\varepsilon=\frac{P_{2}I_{1}^{2}-P_{1}I_{2}^{2}}{I_{1}I_{2}\left(I_{2}-I_{1}\right)}=12\;\text{V}\)
